Abstract
As exoplanetary science matures into its third decade, we are increasingly offered the possibility of pre-existing, archival observations for newly detected candidates. This is particularly poignant for the TESS mission, whose survey spans bright, nearby dwarf stars in both hemispheres—precisely the types of sources targeted by previous radial velocity (RV) surveys. On this basis, we investigated whether any of the TESS Objects of Interest (TOIs) coincided with such observations, from which we find 18 single-planet candidate systems. Of these, one exhibits an RV signature that has the correct period and phase matching the transiting planetary candidates with a false-alarm probability of less than 1%. After further checks, we exploit this fact to validate HD 183579b (TOI-1055b). This planet is <4 R⊕ and has better than 33% planetary mass measurements, thus advancing TESS' primary objective of finding 50 such worlds. We find that this planet is among the most accessible small transiting planets for atmospheric characterization. Our work highlights that the efforts to confirm and even precisely measure the masses of new transiting planet candidates need not always depend on acquiring new observations—in some instances, these tasks can be completed with existing data.
Export citation and abstract BibTeX RIS
1. Introduction
Large-scale photometric surveys have revolutionized our understanding of extrasolar planets through the discovery of thousands of transiting planets (Batalha 2014). Despite the many advantages of the transit method, it suffers from one primary weakness—a planet-like transit can be caused by numerous false positives (Bryson et al. 2013; Santerne et al. 2013; Leuquire et al. 2018).
Determining the true nature of a planet-like transit is complicated by the fact that the false-positive rate (FPR) varies between different photometric surveys; for example, it is ∼10% for Kepler (Borucki et al. 2011) but is far higher for ground-based surveys like KELT (Collins et al. 2018). Of particular interest for this work is the fact that TESS is predicted to have an FPR of ∼40% for the two-minute cadence targets (Sullivan et al. 2015). However, even when one focuses on a specific survey, the FPR varies dramatically with the planetary radius; for example, Kepler's FPR is 17.7% for giant planets but 6.7% for Neptunes (Fressin et al. 2013, but also see Santerne et al. 2012). Moreover, it appear to further depend on the evolutionary state of the parent star (Sliski & Kipping 2014, but also see Gaidos & Mann 2013) and even position within the detector's pixel array (Christiansen et al. 2020).
The "gold standard" solution for distinguishing between genuine transiting planets and false-positives is to obtain radial velocity (RV) measurements that detect the presence of a Doppler signal of the same period and phase as the transit signal (e.g., Hébrard et al. 2019). In the dawning era of thousands of planetary candidates being made available by Kepler, this approach remains powerful—but ultimately limited in impact, due to the challenge of securing the very large number of observing nights required to cover the entire sample. High-significance RV detections are typically described as planet "confirmations" in the associated paper (e.g., Almenara et al. 2018). In some cases, the lack of a detectable RV signal in phase with a known transiter has been used to place upper limits on mass, which is then used as a basis to describe said transiter as "confirmed" (e.g., Timmermann et al. 2020).
Due to the imbalance of RV observations versus transiting planet candidates, alternative strategies have been developed in recent years to make further progress. Specifically, the community has become familiar with the concept of "statistical validation" of planetary candidates. Unlike confirmations, which are implied to be essentially certain planets, validations frame signals as being planets to some probability threshold. These validations generally consider information such as the transit morphology, centroid positions, and high-resolution imaging constraints in the context of both planet and non-planet scenarios (e.g., hierarchical triples), in order to quantify the odds of planethood.
Such validation efforts find their early footing in the work of Torres et al. (2004), who showed that the transiting planet candidate associated with OGLE-TR-33 was likely a false positive. This technique was applied the following year to OGLE-TR-56, which finally led to the first statistically validated planet (Torres et al. 2005).
Statistical validation of transiting planet candidates remained somewhat of a niche exercise in the exoplanet community during those years. This was largely because most transiting planet candidates were coming from ground-based surveys, such as HATNet (Bakos et al. 2004) and WASP (Pollacco et al. 2006), whose targets were bright and not so numerous that RV confirmation was almost ubiquitous in the resulting papers. This situation shifted in the Kepler era, when exoplanet astronomers began drinking from a fire hose and could no longer keep up with the large catalogs of planetary candidates being released (e.g., Borucki et al. 2011). The BLENDER software (Torres et al. 2011) was the first attempt to generalize the validation framework for en masse work and led to the validation of dozens of new Kepler planets (Torres et al. 2015, 2017). In tandem, more computationally efficient validation methods were developed, such as vespa (Morton 2012) and Gaussian Process Classification (Armstrong et al. 2020), enabling the validation of many hundreds of Kepler candidates. The inclusion of planet multiplicity information into the validation methodology by Lissauer et al. (2012) further empowered the approach to the point where the majority of Kepler planetary candidates have now been validated (Rowe et al. 2014; Morton et al. 2016).
Despite the apparently dwindling need for RVs during these years, the value of RV measurements is arguably entering somewhat of a renaissance. Precise RV data sets have now been accumulating for two decades (Butler et al. 2017), revealing the long-period population of exoplanets (e.g., Wittenmyer et al. 2016). Furthermore, the paucity of observed planet masses among the transiting population has highlighted certain needs, such as better constraints on the planetary mass–radius relation (Chen & Kipping 2017), predicting the scale height in transmission spectroscopy work (Anglada-Escudé et al. 2013), and removing degeneracies in exomoon work (Teachey & Kipping 2018). Moreover, the impact of RVs is buoyed by the fact that TESS is focused on brighter stars (Ricker et al. 2015), which are far more amenable to RV characterization than those of Kepler. Indeed, it is telling that a primary goal of the TESS mission is to measure the masses of 50 small ( ≲ 4 R⊕) exoplanets (despite the fact TESS itself generally cannot measure masses).
In the TESS era, then, RVs will clearly play a role far more impactful than that of Kepler, and in this work, we consider to what extent they can be used to validate known transiting planet candidates. In particular, we turn to publicly available archival RV surveys over the last two decades of the northern and southern skies, which include many targets not just observed by TESS but also found to have TOIs (TESS Objects of Interest). Although no planets may have been detectable in the original time series, the inclusion of the TESS ephemerides (which are typically very precisely measured) adds new constraints to these data sets that may elevate signals previously lying beneath the noise floor.
We describe this new approach in Section 2, along with the identification of one newly validated planet. In Section 3, we explore the physical properties of this planet by including the constraints from the transit light curve and stellar isochrones. The importance of this individual planet is discussed in Section 4, along with a broader-brush discussion of this new approach to validating exoplanets.
2. Radial Velocity Analysis
2.1. Cross-referencing TOIs
We begin by curating a list of sources that have RV measurements available, looking in particular for sources that have had no previous planet detections. Although numerous surveys have been published over the years, we limit ourselves to just the largest surveys, in order to provide a degree of catalog homogeneity. Specifically, we seek one large survey in each celestial hemisphere to provide the necessary data. To this end, we identify the Lick–Carnegie Exoplanet Survey (LCES) using the HIRES instrument on Keck I, and the High Accuracy Radial Velocity Planet Searcher (HARPS) mounted on the 3.6 m ESO telescope at La Silla as most suitable.
From LCES, we obtained 60,949 publicly available radial velocities for 1624 unique sources processed and published by Butler et al. (2017). These observations span 20 yr, with an instrument upgrade occurring in 2004 August. Despite this, Butler et al. (2017) report no significant velocity offset after the upgrade in their published RVs, and explicitly state so in their work. Therefore, we will treat the entire data set as originating from a single instrument.
From HARPS, we obtained over 212,000 RVs for 2912 sources (Trifonov et al. 2020). HARPS has been mounted since 2003, but an instrument upgrade in May 2015 introduced an RV offset that needs to be accounted for between these two eras—and it is different for each star (Trifonov et al. 2020).
In rare cases, sources were caught by both surveys. Of the six unique sources for which this was the case, four were already known planet detections, and thus were not impactful to our overall procedure. The remaining two were treated in the same manner as the HARPS upgrade, with an RV offset that needs to be accounted for between the two instruments for each star respectively.
We then proceeded to filter the list down to only sources that were also listed as a TOI via the TESS Alert system, yielding 100 TOIs from 97 sources. Of these, 70 were already known planet detections at the time of writing and so these were excluded from our analysis. We also excluded six TOIs that had five or fewer total RV observations. We also excluded three sources with two TOIs each in the same system, because multi-planet systems are not compatible with our validation methods. For multi-planet TOIs, our validation methodology can not adequately disentangle the signal between the two planet candidates, and thus their inclusion in our analysis is unnecessary. This provides us with a final list of 18 TOIs that have not been confirmed as planets, as of the time of writing, and have archival precise radial velocities available from either HIRES or HARPS. These 18 TOIs are listed in Table 1.
Table 1. Summary of Several Tests Applied to Our TOIs to Identify Statistically Significant and Physically Sound Radial Velocity Solutions
| TOI | Main Identifier | FAP | K RadVel (m s−1) | K forecaster (m s−1) | Kcirc (m s−1) | LS test for K RadVel | Physicality p-value |
|---|---|---|---|---|---|---|---|
| 1055.01 | HD 183579 | 0.32% |
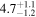
| [1.2, 8.1] | 3.8 | 0.49% | 0.23 |
| 260.01 | GJ 1008 a | 1.2% |
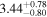
| [0.0, 5.1] | 3.1 | ⋯ | ⋯ |
| 560.01 | GJ 313 | 1.48% |
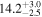
| [2.0,12.3] | 19 | ⋯ | ⋯ |
| 1611.01 | HD 207897 | 2.6% |
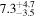
| [0.6, 4.3] | 2.8 | ⋯ | ⋯ |
| 1827.01 | Wolf 437 a | 4.2% |
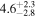
| [0.9, 9.7] | 2.5 | ⋯ | ⋯ |
| 1011.01 | HD 61051 | 9.1% |
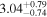
| [0.6, 3.5] | −1.2 | ⋯ | ⋯ |
| 179.01 | HD 18599 | 9.4% |

| [1.5, 8.5] | 18 | ⋯ | ⋯ |
| 440.01 | HD 36152 | 13.0% |
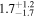
| [1.5, 6.8] | −0.55 | ⋯ | ⋯ |
| 461.01 | HD 15906 | 21.5% |
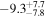
| [1.3, 5.2] | 2.6 | ⋯ | ⋯ |
| 1860.01 | HD 134319 | 34.7% |
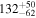
| [0.0, 10.3] | 59 | ⋯ | ⋯ |
| 486.01 | GJ 238 | 50.6% |
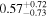
| [0.06,0.18] | 0.61 | ⋯ | ⋯ |
| 909.01 | HD 150139 | 57.8% |
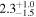
| [0.8, 8.3] | −0.52 | ⋯ | ⋯ |
| 198.01 | GJ 7 | 63.6% |
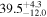
| [0.5, 3.4] | 27.8 | ⋯ | ⋯ |
| 1970.01 | TYC 8647-2057-1 | 78.7% |
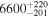
| [42, 18000] | −71 | ⋯ | ⋯ |
| 253.01 | HIP 4468 | 87.1% |
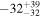
| [0.0, 8.0] | 0.77 | ⋯ | ⋯ |
| 731.01 | GJ 367 | 89.5% |
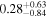
| [0.0, 4.6] | 0.11 | ⋯ | ⋯ |
| 139.01 | HIP 110692 | 91.2% |
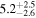
| [1.4, 6.7] | 0.45 | ⋯ | ⋯ |
| 741.01 | GJ 341 | 92.6% |
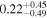
| [0.0,2.0] | 0.054 | ⋯ | ⋯ |
Note.
a An outlier point was removed during the analysis.Download table as: ASCIITypeset image
2.2. A Check for Long-term Trends
Before we can look for the short-period RV signals expected due to the TOIs, it is necessary to check for evidence of long-term trends in the data. If these should exist, a failure to account for them would degrade our sensitivity to detect low-amplitude signals. To accomplish this, we performed a linear least-squares fit of the RV time series using the inverse square of the reported uncertainties as the weights (no jitter is included for this test). A flat, linear, and quadratic trend model are regressed to each time series, from which we compute a χ2 and BIC (Schwarz 1978) score. The model with the lowest BIC is saved as the appropriate trend model for each TOI. To account for the effect of the 2015 upgrade to HARPs on RV data sets with observations that span the eras before and after 2015, we implemented a Nelder–Mead minimization routine to solve piecewise equations accounting for the offset between the RVs from the pre- and post-upgrade time periods corresponding to flat, linear, and quadratic trends. We then follow the stated procedure of choosing the model with the lowest BIC as the correct trend for the given TOI. The same workflow was applied to the TOIs with data from both HARPS and LCES. We note that, while the trend models we adopt are favored by the BIC score for a given TOI, these trends are not necessarily statistically significant. Of the TOIs we determined to have RV data with a linear or quadratic favored trend model, TOIs 486.01, 560.01, 741.01, 198.01, 1860.01, 909.01, 1055.01, 179.01, 1611.01, 440.01, 1011.01, 253.01, and 1970.01 had ΔBIC > 10, indicating a strong likelihood of a trend in their respective RV data.
2.3. Calculating False-alarm Probabilities (FAPs)
We considered several tests to evaluate whether there is a genuine RV signal in the archival data associated with each TOI, but the first of these is a bootstrapping false-alarm probability (FAP) test. This test consists of three steps, described as follows. First, for each TOI, we fit a trend + circular orbit model (which can be expressed as a purely linear model for a given period) to the TOI's RV data, weighting by the inverse square uncertainties, and evaluate the χ2 goodness-of-fit. The trend component of the model corresponds to the BIC best-fit trend; if the BIC for a given RV data set favors a flat trend, only a constant offset term is included, while if the BIC for a given RV data set favors a linear or quadratic trend, linear or quadratic terms are included in addition to the constant offset term. We allow for negative K values during this process, which can be used a diagnostic for "bogus" detections later. For planets on near-circular orbits, which are broadly expected given the short-period nature of the TOIs, one expects the phase-folded RVs to follow an inverted sinusoid of amplitude Kcirc (Kipping 2013a). What this means is that, at the time of inferior conjunction (i.e., mid-transit time), the RV signal should be zero because the star is moving tangentially, but the acceleration should be blueshifting maximally (i.e., the RV gradient is maximally negative). Thus, our linear equation was of the form:
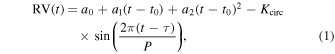
where t0 is a pivot point selected near the midpoint of the observational baseline, and a2, a1, and a0 are constants corresponding to quadratic, linear, and constant trends in the data, respectively. We utilized the linalg.lstsq function from the NumPy PYTHON module to regress Equation (1) to the available RVs for each TOI. Once again, for TOIs with HARPS RV data that span the pre- and post-upgrade eras, as well as the TOIs with data from both HARPS and LCES, we used the nonlinear Nelder–Mead minimization routine to solve the piecewise equation accounting for the constant offset between the two observation periods or the two different instruments.
Since this is a fit, with some parameter flexibility, the resulting χ2 will always be better than that obtained without the sinusoid present. Thus, an improvement in χ2 is not sufficient to claim a detection. Further, the noise properties cannot be assumed to behave as strictly Gaussian, and thus we avoid making detection claims based on the degree to which χ2 improves either. In light of these points, how can one go about evaluating a probability for the reality of these signals?
We approach this through bootstrapping. Specifically, we repeat the same procedure described above, but with a different (and ultimately false) ephemeris. The orbital period is drawn from a probability distribution, which approximates the observed TOI period distribution, but we exclude any periods which are within 20% of the true answer. This approximate distribution was found by first inspecting the distribution the log-periods of the 2330 available TOIs, which exhibit an approximately triangular distribution mixed with a background uniform distribution. We performed likelihood maximization of a uniform+triangular mixture model, with support defined over the range of the available log-periods, yielding a mixture model that is 0.777 triangular, whose shape has a mode at  , a minimum at −0.026 and a maximum at 3.804. After a period is selected from this distribution, the phase is simply randomized uniformly. For each random ephemeris, a linear equation with an inverted sinusoid and trend is fit (or nonlinear piecewise equation for the TOIs, where this is necessary), and the χ2 improvement is recorded. Since the real fit allows negative K values, the exact same procedure and rule set are used for the bootstrap, to keep everything like-for-like.
, a minimum at −0.026 and a maximum at 3.804. After a period is selected from this distribution, the phase is simply randomized uniformly. For each random ephemeris, a linear equation with an inverted sinusoid and trend is fit (or nonlinear piecewise equation for the TOIs, where this is necessary), and the χ2 improvement is recorded. Since the real fit allows negative K values, the exact same procedure and rule set are used for the bootstrap, to keep everything like-for-like.
A FAP score can then be computed by asking how often the fake ephemerides lead to a χ2 improvement that is superior to the improvement obtained with the true ephemeris. This can be quantified using a one-tailed p-value, similarly to the typical bootstrapping applied to periodogram analyses in RV surveys. RV signals driven by stellar activity can occur across a broad range of frequency space, and in general, have no reason to coincide with a series of periodic and statistically significant box-shaped dips that represent a TOI. In this way, by evaluating the power at different random but representative ephemerides, our FAP scores inflate in the presence of such behavior. A consequence of this is that our approach may obtain false negatives, i.e., genuine RV planets that we reject because there is an activity signal present. Nevertheless, we prefer to err on the side of being conservative in this sense when validating planets in this work.
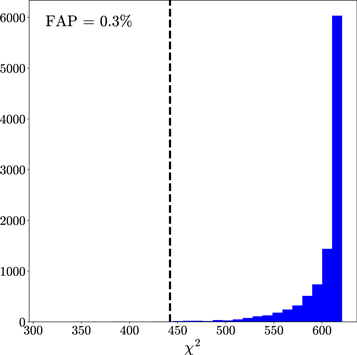
Following the validation work of Morton et al. (2016) on Kepler transiting planets, we consider any FAP score lower than 1% grounds for potential validation (subject to some further checks and tests). The FAP scores are listed in Table 1, where 1 of the 18 TOIs exhibits an FAP below 1%—TOI-1055.01 (HD 183579.01). Figure 1 includes a histogram with the results of the FAP test for this planet.
Figure 1. Results of the FAP test for HD 183579.01. FAP percentage is reported in the upper left corner, and the χ2 value for each true linear fit (using the real P and τ) is denoted by a dashed black line.
Download figure:
Standard image High-resolution imageFour other TOIs exhibit FAP scores below 5%. In this work, these TOIs will not be considered further as candidates for validation, but we note that they are likely planets. These are TOI-260.01 (GJ 1008.01), TOI-560.01 (GJ 313.01), TOI-1611.01 (HD 207897.01), and TOI-1827.01 (Wolf 437.01).
2.4. RadVel Modeling and Testing for Nonzero Semi-amplitudes
To confirm the validity of this TOI as a planet, we conducted a more thorough analysis of its RV data and the light curve of its host star, and then ran two additional tests. In total, 54 RV measurements of HD 183579 were taken by HARPS over the course of 5.5 yr. To analyze these RVs, we utilize the RadVel package (Fulton et al. 2018).
RadVel uses MCMC regression to fit for various physical parameters including P, τ, e (eccentricity), ω (argument of periastron), K, and RV jitter. Since the object is transiting, it will be subject to the eccentricity bias affecting transiting bodies due to geometric probability (Barnes 2007; Burke 2008). This can be formally accounted for by using the e–ω joint prior of Kipping (2014b), specifically their Equation (23). However, the prior is unstable for an intrinsically uniform prior in e, described in α = 1 and β = 1 in that expression. Therefore, we instead use a Beta distribution intrinsic prior for e of α = 1 and β = 2. Formally, the RV population of short-period planets is described better by α = 1 and β = 3, which places more emphasis on low-eccentricity orbits. We elect to set β = 2 in order to create a softer, flatter, and more uninformative prior, yet one that is stable and gently favors more circular orbits. The intrinsic prior on ω is uniform over the the 2π interval.
Since P and τ are strongly constrained from the transit light curve, we employ a Gaussian prior on these terms at their respective TESS ephemeris values. For the RV jitter parameter, σjitter, we employ a broad log-uniform prior from 10% of the median RV error up to twice the range of the RV data. For γ (RV offset),  (RV drift), and
(RV drift), and  (RV curvature), we employ the default RadVel settings of a uniform prior with initial guesses of the median RV value, 0, and 0 m s−1, respectively. The bounds on these terms are set by the range of the RV data in hand. For K, we wanted to ensure that zero-valued and negative solutions were free to be explored, and so we adopt a uniform prior from zero minus twice the range of the RV data to zero plus twice the range of the RV data. The upper and lower limits on this prior are chosen to simply allow any detectable signal with a period shorter than the baseline to be modeled by RadVel.
(RV curvature), we employ the default RadVel settings of a uniform prior with initial guesses of the median RV value, 0, and 0 m s−1, respectively. The bounds on these terms are set by the range of the RV data in hand. For K, we wanted to ensure that zero-valued and negative solutions were free to be explored, and so we adopt a uniform prior from zero minus twice the range of the RV data to zero plus twice the range of the RV data. The upper and lower limits on this prior are chosen to simply allow any detectable signal with a period shorter than the baseline to be modeled by RadVel.
Our RadVel fits use the default mode of running eight independent ensembles in parallel with 50 walkers per ensemble for up to a maximum of 10,000 steps per walker, or until convergence is reached; for further details, see Fulton et al. (2018). We also inspected the posteriors to check for convergence and mixing, and then used them in our calculations of physical properties, along with the transit posteriors. We make these posteriors publicly available at https://github.com/skypalat/toi_validation.
Once the fits were finished, we conducted two basic checks on the marginalized posterior distribution for K. First, if the median of the distribution was negative, the TOI was discarded, which occurred for TOI-461.01 and TOI-253.01. However, we note that neither of these had low FAPs, and thus they would have been rejected regardless. Second, for our TOIs with an FAP score below 1% (which is just TOI-1055.01), we wanted to test whether the K posterior was significantly pulled away from zero, implying a positive detection. Using Bayesian evidences is somewhat unsatisfactory here because those values would strongly depend upon the width of our prior. In particular, for K, there is no obvious upper limit; therefore, it can be increased arbitrarily and thus dilute the Bayesian evidences. Instead, we argue that a better test is the classic Lucy–Sweeney test to evaluate if a parameter is offset from zero (Lucy & Sweeney 1971). The Lucy–Sweeney test returns an FAP that the parameter in question is consistent with zero, which we report in the penultimate column of Table 1. The 1% FAP planet validation threshold of Morton et al. (2016) is again used as a minimum threshold (in addition to the previous tests) for a candidate to be considered validated.
2.5. Statistical Validation of HD 183579b
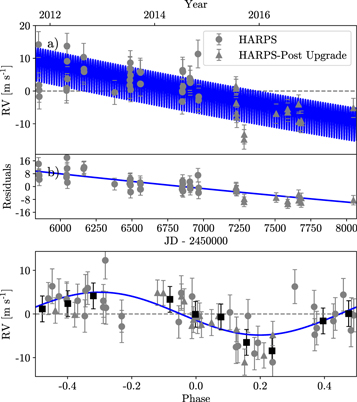
The TOI found earlier (see Section 2.3) to exhibit <1% FAPs with the Monte Carlo test also exhibits a <1% FAP with the Lucy–Sweeney test (see Table 1), as well as positive median K values. Thus, the RadVel solution indicates positive statistical evidence for a signal at the TESS ephemerides for TOI-1055.01. The corresponding RV curves are shown in Figure 2.
Figure 2. RV data fit by RadVel for HD 183579b (TOI-1055b). First and second subplots from the top show RadVel's fit to the raw data and the residuals of those fits. Bottom plot shows RadVel's fits of the phase-folded RV data. Black points in the phase fold plots represent binned data.
Download figure:
Standard image High-resolution imageAs an additional check, we evaluated the one-sided p-value of the a posteriori median K value against the predictions from forecaster—just to ensure that the fits are physically plausible. Since forecaster is an empirical mass–radius relation, this essentially asks whether the implied planetary densities are in the range one would expect for a planet of its size. Once again, this TOI did not have a suspicious p-value (less than 0.05), and thus it appears physically sound.
We also revisited the FAP calculation with consideration of the trend model used. The existence of either a linear or quadratic trend appears statistically secure with BICquad = 636.7 and BIClin = 641.7, but BICflat = 672.8, indicating that ΔBIC > 30. Although the quadratic model is favored over the linear model, we repeated the FAP calculation with a linear model only, and obtained an even better FAP score of 0.22%. The low FAP score thus appears robust between these two competitive trend models.
Finally, we examined the data validation (DV) reports for this TOI in order to confirm that there were no indicators of false positive signals. DV reports are generated by the NASA Science Processing Operations Center (SPOC) pipeline (Jenkins et al. 2016) for threshold-crossing events (TCEs) in short-cadence observations and by the MIT Quick Look Pipeline (QLP; Huang et al. 2020) for TCEs in long-cadence observations (full frame images). TOI-1055.01 has public DV reports from both the SPOC pipeline and the QLP pipeline. We checked these DV reports to look for red flags such as centroid offsets, differences in odd and even transits, or correlation between the flux depth and the aperture size. We again find no reason to suspect the transit signals to be spurious. We also note that the transit signal was independently inspected by Giacalone et al. (2021) who find a 2% FAP from the light curve, not enough to validate but again indicating a likely real planet.
From the passing of these checks in combination with our FAP scoring, we conclude that TOI-1055.01 (HD 183579.01) and is most likely a real planet to >99% confidence. Therefore, we refer to it as statistically validated in what follows—hence updating its moniker to HD 183579b.
2.6. A Note on Outliers
We note that, for several TOIs, the omission of outlier RVs has a noticeable impact on their corresponding FAP score and Lucy–Sweeney results. RVs considered as outliers are at least 6σ from both the favored long-term trend model and the trend + circular fit, and also have large error bars compared to the other RVs. TOI-253.01, while quite far from being validated, saw its FAP score improve by 20% with the omission of an outlier RV. TOI-260.01 and TOI-1827.01 were just on the threshold of validation, with the exclusion of one outlier RV each, but not quite past the >99% benchmark. Nonetheless, these two objects remain highly interesting—and with further observation, may prove to be planets.
3. Transit and Isochrones Analysis
3.1. Stellar Isochrones
To complete our picture of the HD 183579 system, we require fundamental stellar parameters. To this end, we performed a stellar isochrone analysis using the isochrones package by Morton (2015). The isochrones package takes the observable stellar properties as inputs and uses these to derive fundamental properties by matching to stellar evolution models—in our case, we employed the Dartmouth models (Dotter et al. 2008).
As inputs, we start with the apparent magnitude in the V band reported in Koen et al. (2010) and Høg et al. (2000), and in the 2MASS J, H, K bands by Cutri et al. (2003). Next, we searched the literature for stellar atmosphere parameters and elected to use the precise atmosphere parameters reported in Luck (2018), which leverage the public HARPS spectra.
We also used the Gaia DR2 parallax from Luri et al. (2018) as a luminosity indicator. This was included as an extra constraint on the stellar luminosity in the isochrone fits (Bakos et al. 2010). Although our target is bright by exoplanet standards, the brightest magnitude in G for HD 183579 is 8.5, significantly fainter than the G ≲ 5 range highlighted by Drimmel et al. (2019) as exhibiting strong biases. However, we do account for the much smaller systematic parallax error reported by Stassun & Torres (2018). All of these input parameters are listed in Table 2. We ran isochrones (Morton 2015) until 100,000 posterior samples had been generated.
Table 2. Summary of the Stellar Parameters Calculated from the Isochrone Analysis for the Host Star of HD 183579b
| Parameter | Units | HD 183579 (TOI-1055) |
|---|---|---|
| V | V-band Magnitude | 8.68 ± 0.01 |
| J | J-band Magnitude | 7.518 ± 0.023 |
| H | H-band Magnitude | 7.231 ± 0.047 |
| K | K-band Magnitude | 7.150 ± 0.027 |
| Teff | Effective Temperature (K) | 5788 ± 44 |
| Fe/H | Iron-to-Hydrogen Ratio | −0.023 ± 0.050 |

| Surface Gravity | 4.50 ± 0.03 |
| π | Parallax | 17.516 ± 0.066 |
| d | Distance (pc) |
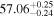
|
| M⋆ | Stellar Mass (M⊙) |
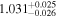
|
| R⋆ | Stellar Radius (R⊙) |
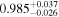
|
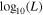
| Log Luminosity |
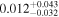
|
| Age | Age (yr) |

|
| ρ⋆ | Stellar Density (g cm−3) |
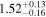
|
Note. The parameters below the horizontal line are the physical dimensions of the stars.
Download table as: ASCIITypeset image
We note that, for this star, we obtain good agreement between the light-curve-derived stellar density and that from our isochrone analysis, with a ratio of 1.06 ± 0.22. Unaccounted for blend sources would cause the ratio of these two to deviate from unity (Kipping 2014a), and if the transits were associated with a completely different star (e.g., in the background), then the difference could be very large. The fact that this case has a density ratio within one sigma of zero (see  row in Table 2) thus provides additional support that this is indeed a genuine planet transiting the target star.
row in Table 2) thus provides additional support that this is indeed a genuine planet transiting the target star.
3.2. Transit Analysis
We further improve our understanding of the validated planet by including an analysis of its transit light curve. We downloaded the two-minute Pre-Data search Conditioning (PDC) light curve for this source from the Mikulski Archive for Space Telescopes (MAST). At the time of writing, TOI-1055b had been observed in Sectors 13 and 27, exhibiting two and one transits respectively.
The light curve was cleaned of time stamps indicating error codes and outliers using moving median filter. We then detrended the light curve of long-term trends following the method marginalization approach described in Kipping et al. (2019). As in that paper, the scatter between different model detrendings is propagated into the updated formal uncertainties on our method marginalized light curve.
The transit light curve was then fit using a nine-parameter Mandel & Agol (2002) forward model coupled to a multimodal nested sampling algorithm, MultiNest (Feroz et al. 2009). Limb darkening was modeled using a quadratic law but reparameterized to the q1–q2 formulation of Kipping (2013b), to enable efficient exploration of the parameter volume. We parameterize the rest of the transit model with seven other terms: the time of transit minimum, τ, the orbital period, P, the impact parameter, b, the ratio of radii, p, the mean stellar density, ρ⋆, the orbital eccentricity, e, and the argument of periastron, ω. For many of these, we adopt a simple uniform prior (q1 ∈ [0, 1], q2 ∈ [0, 1], ![$\tau \in [\hat{\tau }-0.1,\hat{\tau }+0.1]$](https://content.cld.iop.org/journals/2041-8205/909/1/L6/revision3/apjlabe0bbieqn31.gif) ,
, ![$P\in [\hat{P}-0.1,\hat{P}+0.1]$](https://content.cld.iop.org/journals/2041-8205/909/1/L6/revision3/apjlabe0bbieqn32.gif) , b ∈ [0, 2], p ∈ [0, 1]). Note that
, b ∈ [0, 2], p ∈ [0, 1]). Note that  and
and  are the TESS-reported best-fitting ephemeris parameters.
are the TESS-reported best-fitting ephemeris parameters.
Eccentricity and mean stellar density are degenerate in a light-curve fit (Kipping 2014a), and so we use the stellar mean density derived from our isochrone analysis (see Section 3.1) as an informative prior. After trying several different parametric distributions to describe the isochrone-derived stellar density distribution, we found the following provided a good approximation: ![${\rho }_{\star }\sim { \mathcal W }[1563,11]$](https://content.cld.iop.org/journals/2041-8205/909/1/L6/revision3/apjlabe0bbieqn35.gif) kg m−3 (where
kg m−3 (where  is a Weibull distribution). For eccentricity and argument of periastron, we use the same joint prior as described earlier in Section 2.4.
is a Weibull distribution). For eccentricity and argument of periastron, we use the same joint prior as described earlier in Section 2.4.
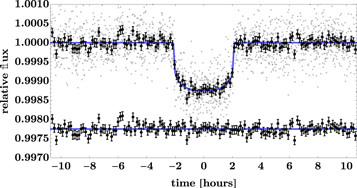
We make the posterior samples publicly available for this regression at the aforementioned GitHub repo. 3 The maximum a posteriori solution is plotted in Figure 3 for HD 183579b. The physical parameters implied by this fit are discussed later in Section 4.1.
Figure 3. Phase-folded transit light curve of HD 183579b (TOI-1055b) as observed by TESS. Black points represent the method marginalized detrended two-minute TESS photometry. Red line shows the maximum a posteriori fit from our regressions. Lower panel shows the residuals between the two.
Download figure:
Standard image High-resolution image3.3. Refined RadVel Fits
Although we have obtained an orbital fit for the radial velocities earlier in Section 2.4, that analysis did not include any eccentricity constraints from the transit fit, because the TOIs remained unvalidated at that time. Having now validated HD 183579b, we rerun the RadVel fit for this planet, including the eccentricity constraints from the transit to improve the overall precision in our final system parameters.
This is accomplished by introducing a modification to the RadVel likelihood function that accounts for this constraint on the orbital eccentricity. The ratio of light-curve-derived stellar density (see Section 3.2) to that from an independent measure—in our case, from isochrones (see Section 3.1)—directly yields  , as shown in Kipping (2010) (see their Equation 39).
, as shown in Kipping (2010) (see their Equation 39).
To implement this constraint, in the logprob function of the RVLikelihood class of the module's likelihood.py file, we added a custom log-likelihood function describing the agreement between each trial's predicted  versus observed
versus observed  (log of the density ratio) value. This was achieved by using a kernel density estimation on the transit
(log of the density ratio) value. This was achieved by using a kernel density estimation on the transit  posteriors that was then used to tabulate a grid of log-like versus
posteriors that was then used to tabulate a grid of log-like versus  , which in turn was approximated with a piecewise fourth-order polynomial with a break at
, which in turn was approximated with a piecewise fourth-order polynomial with a break at  . We sampled this function in a test MCMC to ensure it reproduces the eccentricity distribution from the transits, as expected. This typically helps reduce the amount of time RadVel spends exploring highly eccentric solutions, and it keeps the radial velocity solution in line with that found from the transit analysis (see Section 3.2).
. We sampled this function in a test MCMC to ensure it reproduces the eccentricity distribution from the transits, as expected. This typically helps reduce the amount of time RadVel spends exploring highly eccentric solutions, and it keeps the radial velocity solution in line with that found from the transit analysis (see Section 3.2).
Note that, since we use the posteriors from the transit fit to construct the revised RadVel prior, it is not necessary (nor even allowable) to include the intrinsic Beta prior and transit bias priors from before, as these are already baked into the  posterior.
posterior.
4. Discussion
4.1. Properties of HD 183579b
In this work, we report the validation of one planet orbiting HD 183579, which represents a new exoplanet. A summary table of the physical properties is shown in Table 3.
Table 3. Median and ±38.1% Quantiles of the Joint Posteriors for HD 183579b's Fitted Parameters (top) and Derived Parameters (Bottom)
| Parameter | Value |
|---|---|
| P [days] |
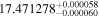
|
| τ [TESS BJD] a |
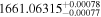
|
| p ≡ RP /R⋆ |
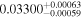
|
| b |

|
| ρ⋆ [g cm−3] |

|
| q1 |
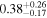
|
| q2 |
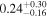
|
| e | <0.28 [2 σ] |
| K [m s−1] |
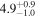
|
| γ [m s−1] |
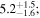
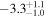
|
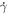 [m s−1 yr−1] [m s−1 yr−1] |
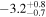
|
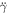 [m s−1 yr−2] [m s−1 yr−2] |
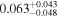
|
| σjitter [m s−1] |

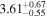
|
| RP [R⊕] |
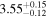
|
| MP [M⊕] |

|
| ρP [g cm−3] |

|
| i [°] |
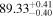
|
| a/R⋆ |
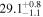
|
| a [au] |
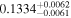
|
| T14 [hr] |

|
| T23 [hr] |
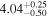
|
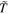 [hr] [hr] |
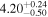
|
| u1 |

|
| u2 |
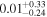
|
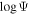
|
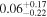
|
| S [S⊕] |

|
| Tblackbody [K] |

|
| TSM |
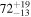
|
Note.
a TESS BJD is equivalent to BJD—2,457,000.Download table as: ASCIITypeset image
HD 183579b orbits the G2V host star HD 183579 located d = (57.37 ± 0.19) pc away in the Telescopium constellation. This star is notably bright in both the optical and infrared at V = 8.67 and K = 7.15, and therefore offers favorable conditions for follow-up observations. From our isochrone analysis, we determine that HD 183579 is (1.03 ± 0.051) M⊙ and (1.022 ± 0.071) R⊙, implying a slightly earlier type than that reported in TIC-8 (1.04 ± 0.14 M⊙ and 0.975 ± 0.055 R⊙; Stassun et al. 2019). The mass, radius, and spectral type of HD 183579 are remarkably similar to those of the Sun. In fact, HD 183579 has been the subject of various analyses of Sun-like stars, including those for chemical abundances (Bedell et al. 2018), infrared excess (Da Costa et al. 2017), and stellar age compared to chemical composition (Tucci Maia et al. 2016). Each of these studies indicates that HD 183579 exhibits the typical properties of a solar twin, including having a spectrum very similar to the Sun.
The RV measurements for this star come from HARPS, with 53 measurements spanning the dates 2011 October 13 to 2017 October 21. We determine that the quadrature jitter term is approximately 3 m s−1, close to the median formal uncertainties for the data set of 1.2 m s−1 and indicating that the star is relatively quiet. The target is flagged as having an "unambiguous" rotational modulation by Canto Martins et al. (2020), with a clear periodicity present in the light curve at 8.8 days. Regressing a sinusoid to the Sector 13 light curve, we obtain an amplitude of 260 ppm, against which there is residual scatter of 420 ppm—consistent with the median formal uncertainty of 409 ppm. In Sector 27, we find almost the same periodicity (8.9 days) of amplitude 240 ppm, against which there is residual scatter of 417 ppm—consistent with the median formal uncertainty of 374 ppm. We thus conclude that the star likely exhibits rotational modulations due to spots, but this activity is small at ∼250 ppm and thus generally consistent with a quiet star.
For HD 183579b, we report with a radius of (3.55 ± 0.13) R⊕, thus placing it firmly in the Neptunian category of Chen & Kipping (2017). We determine a mass for HD 183579b of  M⊕, indicating a bulk density of
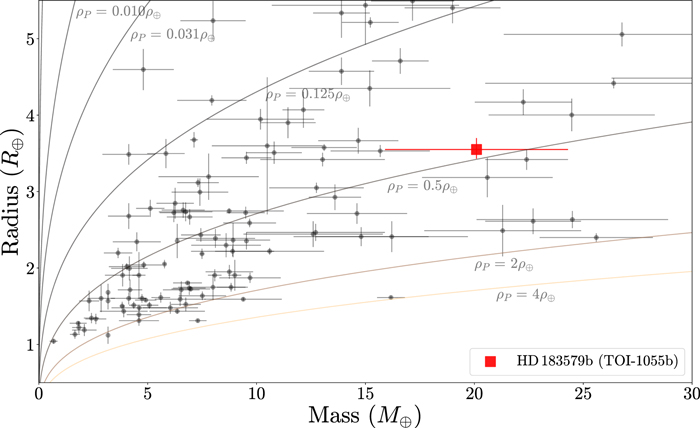
M⊕, indicating a bulk density of  g cm−3. The planetary mass and radius indicate that HD 183579b resembles Neptune/Uranus in bulk density, and perhaps has thus migrated inward from beyond the ice line. Figure 4 is a standard mass–radius diagram demonstrating where HD 183579b falls in a distribution of known planets.
g cm−3. The planetary mass and radius indicate that HD 183579b resembles Neptune/Uranus in bulk density, and perhaps has thus migrated inward from beyond the ice line. Figure 4 is a standard mass–radius diagram demonstrating where HD 183579b falls in a distribution of known planets.
Figure 4. Mass–radius diagram demonstrating where the newly validated planet lies among the population of known planets. HD 183579b is represented by a red square. Contour lines indicate levels of constant density. HD 183579b has dimensions consistent with a Neptunian exoplanet.
Download figure:
Standard image High-resolution imageHD 183579b orbits its host star once every 17.5 days at a semimajor axis of (0.1334 ± 0.0062) au. From the transit morphology, we find that the orbital eccentricity is consistent with a circular path with a median of  . The FAP of this being eccentric using the Lucy & Sweeney (1971) test is 37%, thus favoring a circular orbit. Further, using the Savage–Dickey ratio (Dickey 1971), we compute the Bayes factor between an eccentric-to-circular orbit model to 0.39—again indicating a preference for the circular solution. Using just the transits, we conclude e < 0.66% to 95.45% confidence.
. The FAP of this being eccentric using the Lucy & Sweeney (1971) test is 37%, thus favoring a circular orbit. Further, using the Savage–Dickey ratio (Dickey 1971), we compute the Bayes factor between an eccentric-to-circular orbit model to 0.39—again indicating a preference for the circular solution. Using just the transits, we conclude e < 0.66% to 95.45% confidence.
The transit posteriors imply a constraint on  (median and standard deviation), which is, recall, propagated as a prior constraint on eccentricity in our RadVel fits. From RadVel, the eccentricity constraints are slightly improved by the inclusion of the RV information, yielding
(median and standard deviation), which is, recall, propagated as a prior constraint on eccentricity in our RadVel fits. From RadVel, the eccentricity constraints are slightly improved by the inclusion of the RV information, yielding  , which may suggest some small amount of eccentricity—thus offering clues to this planet's past. However, we caution that neither the Savage–Dickey ratio nor the Lucy–Sweeney test formally favor an elliptical orbit at this point. We conclude that e < 0.27% to 95.45% confidence, and once again remark that an RV trend appears to indicate an outer body with a significance of ΔBIC > 30.
, which may suggest some small amount of eccentricity—thus offering clues to this planet's past. However, we caution that neither the Savage–Dickey ratio nor the Lucy–Sweeney test formally favor an elliptical orbit at this point. We conclude that e < 0.27% to 95.45% confidence, and once again remark that an RV trend appears to indicate an outer body with a significance of ΔBIC > 30.
From our measured mass and radius, we calculate a transmission spectroscopy metric (TSM) for HD 183579b using Equations (1) and (2) of Kempton et al. (2018) to indicate the expected signal-to-noise ratio for future James Webb Space Telescope (JWST) measurements. Our calculated TSM =  indicates that HD 183579b is a promising object for future JWST observations.
indicates that HD 183579b is a promising object for future JWST observations.
4.2. The Use of Archival RVs
Using exclusively publicly available resources, we were able to validate and characterize the physical properties of one Neptune-sized exoplanet, HD 183579b. Thus, existing data advance TESS's primary objective of measuring the masses and radii of 50 small (<4 R⊕) exoplanets (Ricker et al. 2015).
The planet itself is a fascinating world that will likely be among the rare planets observed by JWST, thanks to its small size and excellent observability. However, we would also like to highlight that the technique used to validate this object could be extended and utilized in the future. For example, we did not consider multiple planet systems in this work, as the FAP scoring system would require some modification to handle the multiple periodicities. Nevertheless, multiples are intrinsically more likely to be genuine planets (Lissauer et al. 2012) and thus would need less of a nudge, in the sense of probability, to become validated planets. Our work highlights the great power of legacy RV surveys in synergy with active missions such as TESS. Furthermore, it demonstrates that the knee-jerk reaction of going to the telescope to get new data is not always necessary: in some cases, existing archives may in fact already serve the desired goal.
D.K. acknowledges support from Columbia's Data Science Institute. The Cool Worlds group thanks Tom Widdowson, Mark Sloan, Douglas Daughaday, Andrew Jones, Jason Allen, Marc Lijoi, Elena West, Tristan Zajonc, Chuck Wolfred, Lasse Skov, Geoff Suter, Max Wallstab, Methven Forbes, Stephen Lee, Zachary Danielson, and Vasilen Alexandrov.
This research has made use of the NASA Exoplanet Archive, which is operated by the California Institute of Technology, under contract with the National Aeronautics and Space Administration under the Exoplanet Exploration Program.
This research has made use of the SIMBAD database, operated at CDS, Strasbourg, France.
This work has made use of data from the European Space Agency (ESA) mission Gaia, 4 processed by the Gaia Data Processing and Analysis Consortium (DPAC 5 ). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement.
This paper includes data collected with the TESS mission, obtained from the MAST data archive at the Space Telescope Science Institute (STScI). Funding for the TESS mission is provided by the NASA Explorer Program. STScI is operated by the Association of Universities for Research in Astronomy, Inc., under NASA contract NAS 526555.
We acknowledge the use of public TESS Alert data from pipelines at the TESS Science Office and at the TESS Science Processing Operations Center.
We are deeply grateful to the HARPS team at Observatoire de Genève, Observatoire de Haute-Provence, Laboratoire d'Astrophysique de Marseille, Service d'Aéronomie du CNRS, Physikalisches Institut de Universität Bern, ESO La Silla, and ESO Garching, who built and maintained the HARPS instrument and were generous enough to make the data public.
Research at the Lick Observatory is partially supported by a generous gift from Google. Some of the data presented herein were obtained at the W.M. Keck Observatory, which is operated as a scientific partnership among the California Institute of Technology, the University of California, and NASA. The Observatory was made possible by the generous financial support of the W.M. Keck Foundation.
We thank all of the observers who spent countless nights using both the HARPS and LCES facilities to collect the data presented here, as well as all of the PIs who submitted telescope proposals year after year to allow the acquisition of these data.
Finally, the authors wish to recognize and acknowledge the very significant cultural role and reverence that the summit of Maunakea has always had within the indigenous Hawaiian community. We are most fortunate to have benefited from the observations obtained from this mountain.
Facilities: Keck I (HIRES), TESS, HARPS.
Software: emcee (Foreman-Mackey et al. 2013), MultiNest (Feroz et al. 2009), RadVel (Fulton et al. 2018), forecaster (Chen & Kipping 2017), isochrones (Morton 2015).
Footnotes
- 3
- 4
- 5